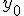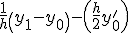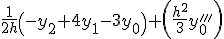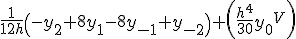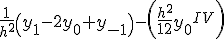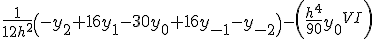Один из широко применяемых методов дифференцирования таблично заданной функции состоит в том, что по узловым (табличным) точкам строится интерполяционный многочлен, а затем вычисляется производная этого многочлена. Например, формулы численного дифференцирования могут быть получены их интерполяционного многочлена Лагранжа. Для многочлена второго порядка, построенного по трем точкам (x_i, y_i), i = 0, 1, 2,

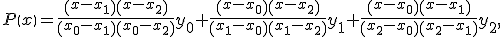
легко получить производную

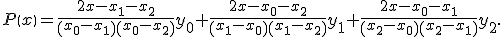
Если это выражение вычислить при x=x₀, то получим значение производной по правым разностям, при x=x₁ – по центральным разностям, а при x=x₂ – по левым разностям.
Для того чтобы получить более точные значения производной используют интерполяционные многочлены высоких порядков.
Расчетные формулы сильно упрощаются в случае, если шаг табулирования функции постоянен (x_i+1 – x_i = h = const).
В таблицах приведены наиболее часто используемые формулы вычисления первой и второй производных таблично заданной функции. Приводятся также значения погрешностей (главная часть) указанных формул.

Приближенные формулы дифференцирования правых разностей

Производные	Вторые разности	Третьи разности

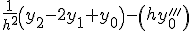Приближенные формулы дифференцирования центральных разностей

Производные	Третьи разности	Пятые разности

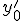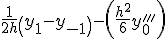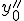 Приближенные формулы дифференцирования левых разностей

Производные	Вторые разности	Третьи разности
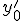
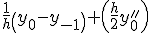
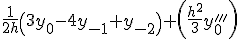
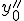